DataLab 保姆级详解¶
约 1723 个字 68 行代码 2 张图片 预计阅读时间 9 分钟 共被读过 次
1. 环境搭建¶
建议使用纯净的 Linux 系统。
本人采用了 Docker 来构建 Ubuntu 系统，这是教程。按照该教程，你可以轻松地在自己的机器上搭建起一个适用于 DataLab 实验的 Ubuntu 环境。
2. 前期准备¶
仔细阅读文件夹中的 README 文件，常用的指令如下：
1. 语法检查：使用 unix> ./dlc bits.c 指令对 bits.c 文件进行语法检查。如果执行该指令后没有任何返回信息，这就表明 bits.c 文件中没有语法错误。
2. 重新编译：每次对 bits.c 文件进行更改后，都需要重新编译 btest 程序。可以使用 unix> make btest 指令来完成这个操作。
3. 题目检测：使用 unix> ./btest 指令来检测所有题目的答案是否正确。该指令会运行一系列的测试用例，帮助你验证自己的代码实现是否符合要求。
3. 开始解题¶
3.1 bitXor¶
描述¶
/*
* bitXor - x^y using only ~ and &
* Example: bitXor(4, 5) = 1
* Legal ops: ~ &
* Max ops: 14
* Rating: 1
*/
本题要求仅使用非门
~ 和与门 & 来实现异或门 ^。 思路¶
异或操作可以用以下三种方式表示：
如果觉得上述表示方式比较突兀，可以从 “集合” 的角度来理解异或操作。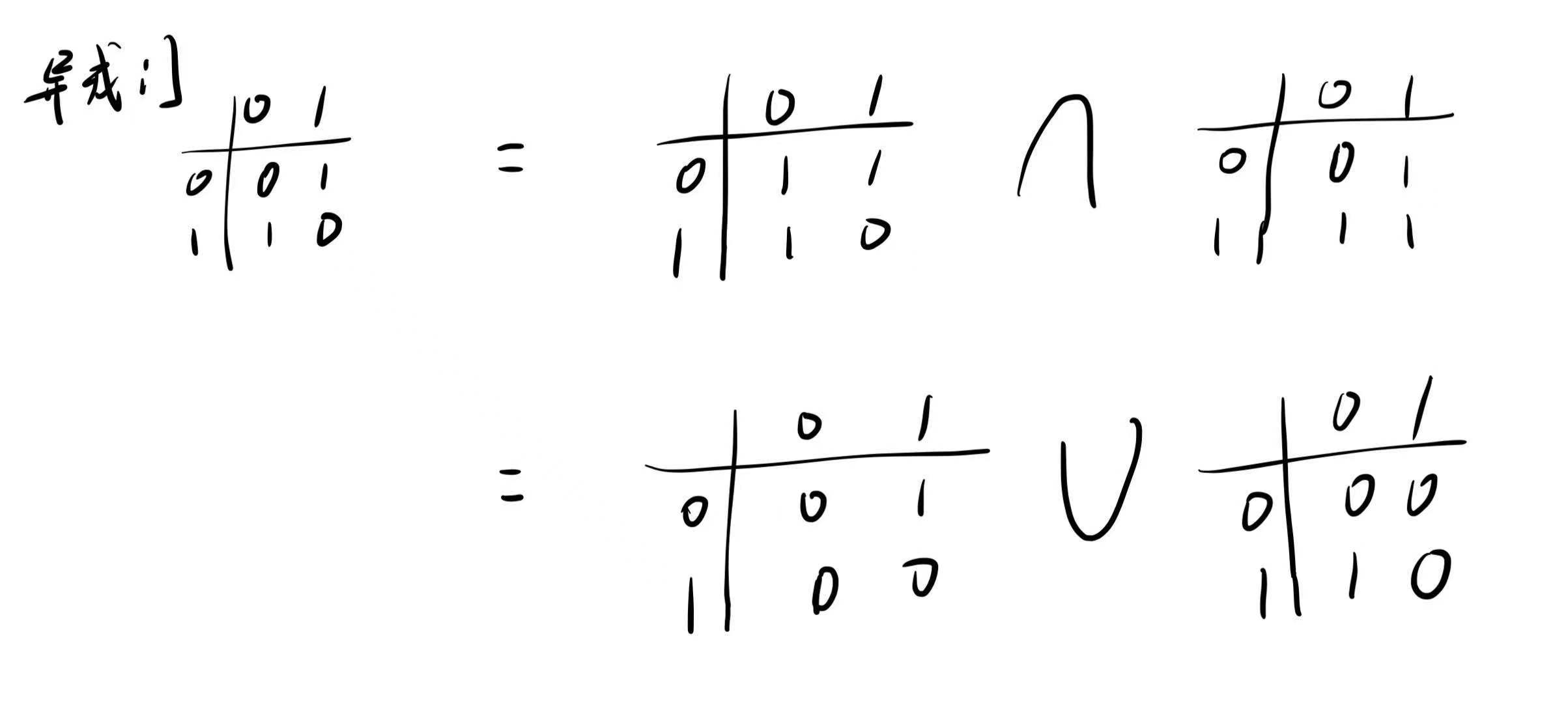
答案¶
3.2 tmin¶
描述¶
/*
* tmin - return minimum two's complement integer
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 4
* Rating: 1
*/
本题要求返回最小的二进制补码整数。在二进制补码表示中，最小的整数是最高位为 1，其余位为 0 的数。
思路¶
最小的二进制整数的特征是只有最高位为 1。我们可以通过将 1 左移 31 位来得到这个数。
答案¶
3.3 isTmax¶
描述¶
/*
* isTmax - returns 1 if x is the maximum, two's complement number,
* and 0 otherwise
* Legal ops: ! ~ & ^ | +
* Max ops: 10
* Rating: 1
*/
本题要求判断一个数
x 是否为二进制补码表示中的最大值。 思路¶
在二进制补码表示中，最大值是 0111...111。它有一个重要的特征：x + 1 后会变成 1000...000，对 x + 1 按位取非会得到 0111...111，即等于 x。我们可以利用异或操作来判断两个数是否相等，因为自己与自己异或会得到 0。
但是，有一个例外情况需要注意，当 x = -1 时，x + 1 = 0，按位取非后也等于 x，但 -1 并不是最大值。所以我们需要排除这种情况。
答案¶
3.4 allOddBits¶
描述¶
/*
* allOddBits - return 1 if all odd-numbered bits in word set to 1
* where bits are numbered from 0 (least significant) to 31 (most significant)
* Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 12
* Rating: 2
*/
本题要求判断一个数的所有奇数位（从右到左依次编号为 0、1、2、3...）是否都为 1。
思路¶
我们可以找到一个典型的数 0xAAAAAAAA，它的奇数位全为 1，偶数位全为 0。如果 x & 0xAAAAAAAA == 0xAAAAAAAA，就说明 x 的每一个奇数位都是 1。
由于题目规定不能直接定义 8 位以上的数，我们需要通过一些技巧来构造 0xAAAAAAAA。可以先定义一个 8 位的数 0xAA，然后通过左移和按位或操作来得到 32 位的 0xAAAAAAAA。
答案¶
int allOddBits(int x)
{
int num = 0xAA;
num = num << 8 | num;
num = num << 16 | num;
return !((x & num) ^ num);
}
3.5 negate¶
描述¶
/*
* negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
*/
本题要求返回一个数的相反数。
思路¶
取反加一
答案¶
3.6 isAsciiDigit¶
描述¶
/*
* isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
*/
本题要求判断一个数是否在 ASCII 码中字符 '0' 到 '9' 的范围内（即 0x30 <= x <= 0x39）。
思路¶
直接判断 0x30 <= x <= 0x39 不太容易实现，我们可以将其转换为和 0 比较的形式。分别计算 x - 0x30 和 0x39 - x，如果这两个结果都大于等于 0，就说明 x 在指定范围内。负数的最高位是 1，我们可以通过右移 31 位来判断一个数是否为负数。
答案¶
int isAsciiDigit(int x)
{
int a = 0x30, b = 0x39;
int num1 = x + (~a + 1); // x - a
int num2 = b + (~x + 1); // b - x
return !num1 | !num2 | (!(num1 >> 7) & !(num2 >> 7));
}
3.7 conditional¶
描述¶
/*
* conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
*/
本题要求实现一个条件运算符，功能等同于 x ? y : z，即如果 x 不为 0，则返回 y；否则返回 z。
思路¶
我们可以根据 x 是否为 0 来生成两个掩码。当 x 不为 0 时，一个掩码全为 1，另一个掩码全为 0；当 x 为 0 时，两个掩码的情况相反。然后分别用这两个掩码与 y 和 z 进行按位与操作，最后将结果相加。
答案¶
3.8 isLessOrEqual¶
描述¶
/*
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
本题要求判断 x 是否小于等于 y，如果是则返回 1，否则返回 0。
思路¶
我们分两种情况来考虑：
1. 当 x 是负数，y 是正数时，x 一定小于 y。
2. 计算 x - y，如果 x - y = 0 或者 x - y < 0，则 x 小于等于 y。
答案¶
int isLessOrEqual(int x, int y)
{
int case1 = x >> 31 & !(y >> 31); // case1: x是负数，y是正数
int num = x + (~y + 1); // x - y
int case2 = !num | (!!(num >> 31)); // case2:x-y=0或者x-y<0
return case1 | case2;
}
3.9 logicalNeg¶
描述¶
/*
* logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
本题要求不使用逻辑非运算符
! 来实现逻辑非的功能。 思路¶
我们可以利用一个数和它的相反数的特性。对于非零数，它和它的相反数的最高位至少有一个为 1；而对于 0，它和它的相反数都是 0，最高位为 0。我们可以通过按位或操作得到一个数，然后判断它的最高位是否为 0。
答案¶
int logicalNeg(int x)
{
int negate = ~x + 1; // negate = -x
int num = x | negate; // 只有当x=0时，最高位为0
return (num >> 31) + 1; // x=0时，num最高位0,return 1
// x!=0 num最高位1,return 0
}
3.10 howManyBits¶
描述
/* howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
思路
- 题目要求实现一个
howManyBits 函数，用于返回用补码表示一个整数 x 所需的最少位数。一开始看到最大操作数限制为 90（Max ops: 90），很容易想到使用暴力解法。通过循环，对 x 进行右移操作，使用 !!(x >> i) 来判断第 i 位是否为 1，然后将这些结果累加，其中 i 从 1 到 31。然而，这种方法会导致操作数超过限制，因为循环和判断操作会消耗大量的操作数。为了优化算法，我想到可以采用二分搜索的思想。- 使用
!!(x >> 16) 来判断 x 的高 16 位是否存在 1。x >> 16 将 x 右移 16 位，把高 16 位移到低 16 位，然后使用 !! 操作将结果转换为布尔值（0 或 1）。再将这个布尔值左移 4 位（相当于乘以 16），得到 b16。如果高 16 位存在 1，则 b16 为 16；否则为 0。（我当时没想到左移4位这个操作，所以答案借鉴了网上的思路）- 对于负数，在补码表示下，其最高位是 1，并且负数的补码形式不利于直接确定最高位 1 的位置。我们可以利用位运算将负数转换为对应的正数形式。通过
x >> 31 得到符号位信息，如果 x 是负数，x >> 31 的结果为全 1（即 -1）；如果 x 是正数，结果为全 0。- 使用
(flag & ~x) | (~flag & x) 进行处理，当 x 为负数时，相当于对 x 按位取反；当 x 为正数时，x 保持不变。这样就统一了正数和负数的处理方式，方便后续查找最高位 1 的位置。答案
int howManyBits(int x)
{
int b16, b8, b4, b2, b1, b0;
int flag = x >> 31;
x = (flag & ~x) | (~flag & x); // x为非正数则不变 ,x 为负数 则相当于按位取反
b16 = !!(x >> 16) << 4; // 如果高16位不为0,则我们让b16=16
x >>= b16; // 如果高16位不为0 则我们右移动16位 来看高16位的情况
// 下面过程基本类似
b8 = !!(x >> 8) << 3;
x >>= b8;
b4 = !!(x >> 4) << 2;
x >>= b4;
b2 = !!(x >> 2) << 1;
x >>= b2;
b1 = !!(x >> 1);
x >>= b1;
b0 = x;
b0 = x;
return b16 + b8 + b4 + b2 + b1 + b0 + 1;
}
剩下3道float的题，我还没学到，先欠着