CacheLab Learning Log

This log documents my learning process and implementation details for the CS:APP CacheLab. For preparing CET-6, I will try to finish it in English. The lab consists of two parts: Part A involves writing a cache simulator that analyzes memory trace files, and Part B focuses on optimizing matrix transpose performance by exploiting cache locality.

Preparation

• The core of trace files is to record memory accesses. As demonstrated, the Linux command valgrind --log-fd=1 --tool=lackey -v --trace-mem=yes ls -l records every memory access, including instruction loads, data loads, data stores, and data modifications. An example output is shown below: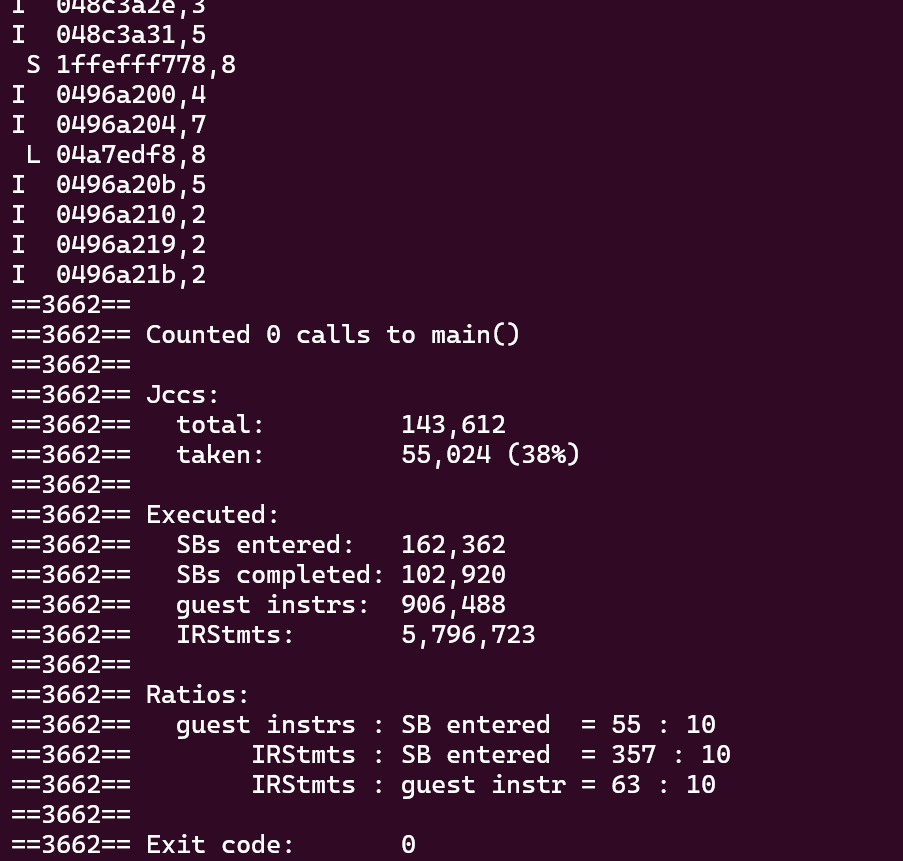
• The format of each line is: [space]operation address,size.
• I denotes an instruction load, L a data load, S a data store, and M a data modify (which is a load followed by a store to the same address).
• There is a space before each M, L, and S operation. The address specifies a 64-bit hexadecimal memory address.

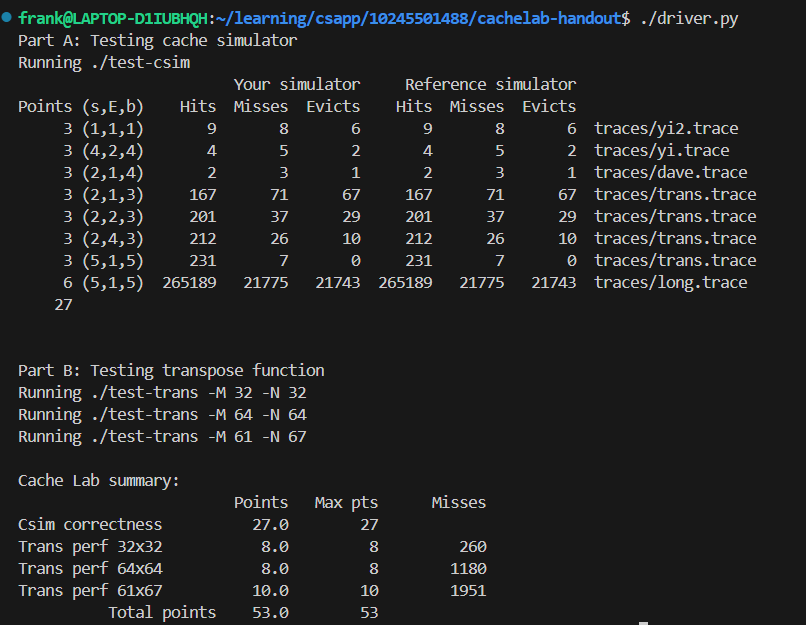
Part A: Writing a Cache Simulator

Key Points

1. In this part, we implement a cache simulator in csim.c. This program takes a valgrind memory trace as input, simulates cache behavior, and outputs the total number of hits, misses, and evictions.
2. The reference simulator, csim-ref, models cache behavior. It accepts the following command-line arguments:
   • -h: Optional help flag.
   • -v: Optional verbose flag for detailed trace output.
   • -s <s>: Number of set index bits (defines S = 2^s sets).
   • -E <E>: Associativity (number of lines per set).
   • -b <b>: Number of block offset bits (defines block size B = 2^b bytes).
   • -t <tracefile>: Path to the memory trace file.
3. The goal for Part A is to make csim.c accept the same command-line arguments and produce identical output to the reference simulator.
4. Include your name and student ID in the header comment of csim.c.
5. The code must compile without warnings.
6. Use malloc to allocate memory for the cache structure so it works correctly for arbitrary s, E, and b.
7. Ignore all instruction cache accesses (lines starting with I).
8. Call the provided printSummary function with the final counts: printSummary(hit_count, miss_count, eviction_count).
9. Request sizes (the number after the comma in the trace) can be ignored for simulation.
10. Use csim-ref to obtain correct answers for validation. The -v option shows a detailed record of each hit/miss/eviction.
11. Start debugging with small trace files like dave.trace.
12. Implement an optional -v argument to enable verbose output for comparing your simulator's behavior with the reference.
13. The getopt function is useful for parsing command-line arguments. Use man 3 getopt for details. An example: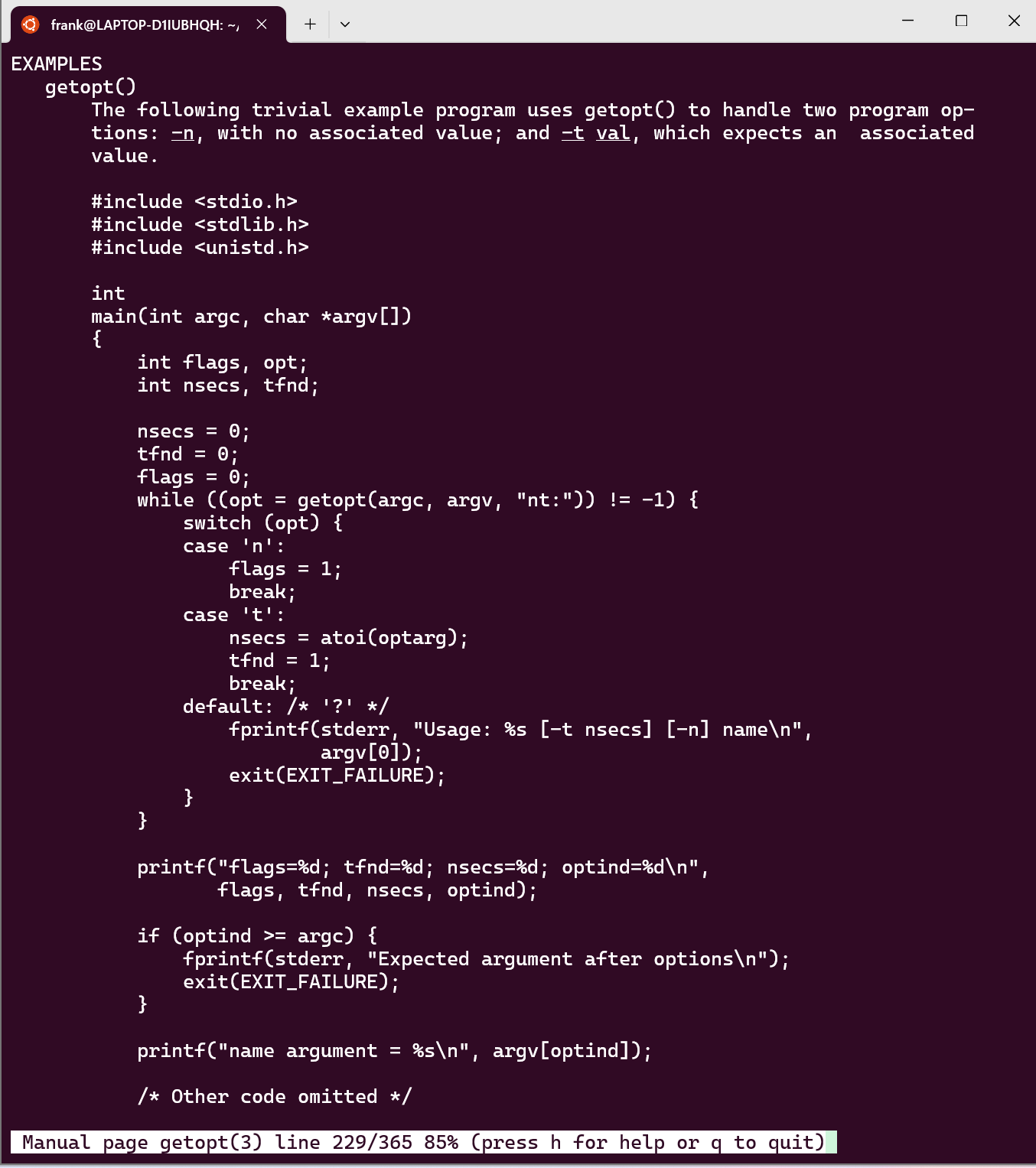
14. Important Cache Behavior:
    • Each data load (L) or store (S) operation can cause at most one cache miss.
    • A data modify (M) operation is treated as a load followed by a store to the same address. Therefore, an M operation can result in:
      • Two cache hits, or
      • One miss and one hit (plus a possible eviction if the set is full and the Least Recently Used (LRU) block needs to be replaced).

Implementation Steps

Step 1: Parse Command-Line Arguments

Parse arguments to configure the cache (s, E, b) and get the trace file path. Use getopt to handle options.

void parseArgument(int argc, char *argv[])
{
    int opt; // Holds the current parsed option character

    // Parse options: "v" for verbose, "s:", "E:", "b:", "t:" for arguments
    while ((opt = getopt(argc, argv, "vs:E:b:t:")) != -1)
    {
        switch (opt)
        {
            case 'v':
                verboseFlag = true;
                break;
            case 's':
                s = atoi(optarg); // Set index bits
                break;
            case 'E':
                E = atoi(optarg); // Associativity (lines per set)
                break;
            case 'b':
                b = atoi(optarg); // Block offset bits
                break;
            case 't':
                traceFile = optarg; // Trace file path
                break;
            default:
                // Handle invalid options or missing arguments
                fprintf(stderr, "Usage: %s [-v] -s <s> -E <E> -b <b> -t <tracefile>\n", argv[0]);
                exit(EXIT_FAILURE);
        }
    }
}

Step 2: Define the Cache Structure

Define a structure for a cache line and allocate a 2D array to represent the cache (sets × lines per set).

typedef struct
{
    int valid;               // Valid bit (1 if line holds data)
    unsigned long long tag;  // Tag bits
    int last_use_time;       // For implementing LRU replacement policy
} cacheLine;

cacheLine **cache; // Dynamic 2D array: cache[sets][E]

Step 3: Allocate Memory for the Cache

Allocate memory based on the configuration parameters.

int setsNum = 1 << s; // Total number of sets: S = 2^s
cache = malloc(sizeof(cacheLine *) * setsNum);
if (cache == NULL) { /* handle error */ }
for (int i = 0; i < setsNum; i++)
{
    cache[i] = malloc(sizeof(cacheLine) * E);
    if (cache[i] == NULL) { /* handle error */ }
    for (int j = 0; j < E; j++)
    {
        cache[i][j].valid = 0;
        cache[i][j].tag = 0; // Initialize tag to 0, not -1
        cache[i][j].last_use_time = 0;
    }
}

Step 4: Simulate Memory Accesses

Read the trace file line by line, parse each operation, and simulate its effect on the cache.

FILE *file = fopen(traceFile, "r");
if (file == NULL) { /* handle error */ }

char operation; // 'I', 'L', 'S', 'M'
unsigned long address;
int size; // Ignored but parsed
while (fscanf(file, " %c %lx,%d", &operation, &address, &size) == 3)
{
    timestamp++; // Global counter for LRU

    switch (operation)
    {
        case 'I':
            // Ignore instruction loads
            break;
        case 'M':
            // Modify = Load + Store to same address
            accessMemory(address);
            accessMemory(address);
            break;
        case 'L':
        case 'S':
            // Load or Store
            accessMemory(address);
            break;
    }
}
fclose(file);

Step 5: Implement the accessMemory Function

This is the core simulation logic for a single memory access.

void accessMemory(unsigned long address)
{
    // 1. Extract cache parameters from the address
    //    Block offset is not needed for finding set/tag.
    int setIndex = (address >> b) & ((1 << s) - 1);
    unsigned long long tag = address >> (b + s);

    cacheLine *set = cache[setIndex];
    int lru_index = 0;      // Index of the least recently used line in this set
    int empty_index = -1;   // Index of the first empty line in this set
    int found = 0;          // Flag for hit

    // 2. Search the set for the tag (hit detection) and find LRU/empty slots
    for (int i = 0; i < E; i++)
    {
        if (set[i].valid)
        {
            if (set[i].tag == tag)
            {
                // Hit: update LRU timestamp and return
                hit_count++;
                set[i].last_use_time = timestamp;
                if (verboseFlag) printf(" hit");
                return;
            }
            // Track the least recently used valid line
            if (set[i].last_use_time < set[lru_index].last_use_time)
            {
                lru_index = i;
            }
        }
        else
        {
            // Track the first empty line
            if (empty_index == -1) empty_index = i;
        }
    }

    // 3. If we reach here, it's a miss
    miss_count++;
    if (verboseFlag) printf(" miss");

    // 4. Handle the miss: place the block in the cache
    cacheLine *line_to_use;
    if (empty_index != -1)
    {
        // Case A: There is an invalid (empty) line
        line_to_use = &set[empty_index];
    }
    else
    {
        // Case B: Set is full, evict the LRU line
        eviction_count++;
        line_to_use = &set[lru_index];
        if (verboseFlag) printf(" eviction");
    }

    // 5. Update the cache line with new data
    line_to_use->valid = 1;
    line_to_use->tag = tag;
    line_to_use->last_use_time = timestamp;
}

Part B: Optimizing Matrix Transpose

Key Points and Constraints

• Goal: Minimize cache misses in the transpose of matrices of varying sizes (32x32, 64x64, 61x67).
• Cache parameters are fixed: s = 5, E = 1, b = 5.
  • This means: 32 sets (S=2^5), direct-mapped (E=1), 32-byte blocks (B=2^5).
  • A 32-byte block can hold 8 int values (assuming 4-byte int).
  • Total cache size: 32 sets * 1 line/set * 32 bytes/line = 1024 bytes.
• Strict coding constraints in trans.c:
  • Use at most 12 local variables of type int.
  • No other data types like long or bit tricks to store multiple values.
  • No recursion.
  • Do not modify matrix A. Only modify matrix B.
  • No additional arrays or matrices allocated with malloc.

Initial Analysis

From the tracegen.c source, we can infer the addresses of matrices A and B. Calculating their offset: 256 * 256 * 4 = 0x40000 bytes. This offset is an exact multiple of the total cache size (1024 bytes). Consequently, elements at the same coordinate in matrices A and B map to the exact same cache set and line. This leads to severe cache thrashing and a very low hit rate for naive transpose implementations.

32x32 Matrix Optimization

Step 1: Basic Blocking The first idea is to use blocking, dividing the matrix into smaller sub-blocks that fit better in the cache. Since a block holds 8 ints, an 8x8 block is a natural size.

// Basic 8x8 blocking
for (int i = 0; i < 32; i += 8) {
    for (int j = 0; j < 32; j += 8) {
        for (int x = 0; x < 8; x++) {
            for (int y = 0; y < 8; y++) {
                B[j + y][i + x] = A[i + x][j + y];
            }
        }
    }
}

Step 2: Handling Diagonal Blocks with Temporary Variables The core idea is to temporally separate accesses to A and B for diagonal blocks. Read an entire row of A's diagonal block into local variables before writing to B, avoiding simultaneous occupancy of the same cache set.

int tmp0, tmp1, tmp2, tmp3, tmp4, tmp5, tmp6, tmp7;
for (int i = 0; i < 32; i += 8) {
    for (int j = 0; j < 32; j += 8) {
        if (i == j) {
            // Diagonal block: use temporaries
            for (int x = 0; x < 8; x++) {
                // Read entire row from A into temporaries
                tmp0 = A[i + x][j];     tmp1 = A[i + x][j + 1];
                tmp2 = A[i + x][j + 2]; tmp3 = A[i + x][j + 3];
                tmp4 = A[i + x][j + 4]; tmp5 = A[i + x][j + 5];
                tmp6 = A[i + x][j + 6]; tmp7 = A[i + x][j + 7];
                // Write temporaries to the corresponding *column* in B
                B[j][i + x] = tmp0;     B[j + 1][i + x] = tmp1;
                B[j + 2][i + x] = tmp2; B[j + 3][i + x] = tmp3;
                B[j + 4][i + x] = tmp4; B[j + 5][i + x] = tmp5;
                B[j + 6][i + x] = tmp6; B[j + 7][i + x] = tmp7;
            }
        } else {
            // Non-diagonal block: direct transpose (no conflict)
            for (int x = 0; x < 8; x++) {
                for (int y = 0; y < 8; y++) {
                    B[j + y][i + x] = A[i + x][j + y];
                }
            }
        }
    }
}

Step 3: Further Optimization - In-Block Transpose The non-diagonal block access B[j+y][i+x] is still column-major within its 8x8 block, which has poor spatial locality (accesses are 128 bytes apart). We can improve by making all accesses row-major through a two-step process: 1) Copy A's rows to B's rows, 2) Transpose within B's block.

// This is a conceptual description. The final, optimal 32x32 code often combines
// these ideas into a single, tight loop using 12 variables.
// 1. Copy A's 8x8 block into B's 8x8 block, but *transposed within 4x4 sub-blocks*
// 2. Perform local swaps inside B to complete the full 8x8 transpose.

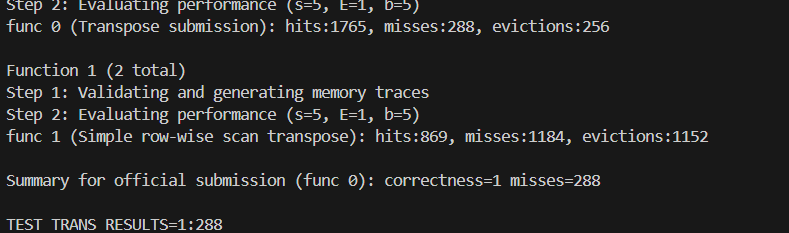
64x64 Matrix Optimization

Using the 8x8 blocking strategy from the 32x32 case results in ~3300 misses on a 64x64 matrix, far from the target (<1300). The reason is that a 64x64 row is 256 bytes. Four such rows (1024 bytes) fill the entire cache. The 8x8 blocks of A and B are now spaced such that they conflict not just on the diagonal, but in many more patterns, thrashing the cache.

Strategy: 8x8 Block with Internal 4x4 Sub-blocks We treat each 8x8 block as four 4x4 quadrants (Top-Left TL, Top-Right TR, Bottom-Left BL, Bottom-Right BR). The goal is to process them in an order that maximizes reuse of cache lines once they are loaded. 1. Process Top Half (Rows 0-3 of A's 8x8 block): * Load the entire top row of the 8x8 block from A (8 ints). * Immediately store the first 4 ints (TL) into their correct, transposed position in B's TL quadrant. * Store the last 4 ints (TR) into a temporary, non-transposed location in B's TR quadrant. This avoids evicting the useful TL lines from the cache. 2. Process Bottom Half (Rows 4-7 of A's 8x8 block): * Load the first column of A's BL quadrant (4 ints). * Swap: Move the temporarily stored data from B's TR quadrant to its final transposed position in B's BL quadrant. * Place the just-loaded A's BL data into its final transposed position in B's TR quadrant. 3. Process Bottom-Right (BR) Quadrant: Finally, transpose A's BR quadrant directly into B's BR quadrant. At this point, the necessary cache lines are already in place with minimal conflict.

This intricate dance ensures that when a cache line is loaded with useful data (e.g., a row from A's TL), it is fully utilized for multiple writes to B before being potentially evicted.

// Conceptual structure of the optimized 64x64 transpose
for (int i = 0; i < 64; i += 8) {
    for (int j = 0; j < 64; j += 8) {
        // Process Top 4 rows (TL & TR of A)
        for (int k = i; k < i + 4; k++) {
            // Load A[k][j..j+7] into 8 temporaries
            // Store first 4 to B[j..j+3][k] (transpose TL)
            // Store last 4 to B[j..j+3][k+4] (temporary hold for TR)
        }
        // Process Bottom 4 rows (BL & BR of A)
        for (int l = 0; l < 4; l++) {
            // Load A[i+4+l][j..j+3] (BL) into 4 temporaries
            // Load the temporary values from B[j+l][i+4..i+7] (our held TR data)
            // Store BL temporaries -> B[j+l][i+4..i+7] (final TR)
            // Store loaded TR data -> B[j+4+l][i..i+3] (final BL)
        }
        // Process BR quadrant
        for (int k = i + 4; k < i + 8; k++) {
            // Load A[k][j+4..j+7]
            // Store to B[j+4..j+7][k] (transpose BR)
        }
    }
}

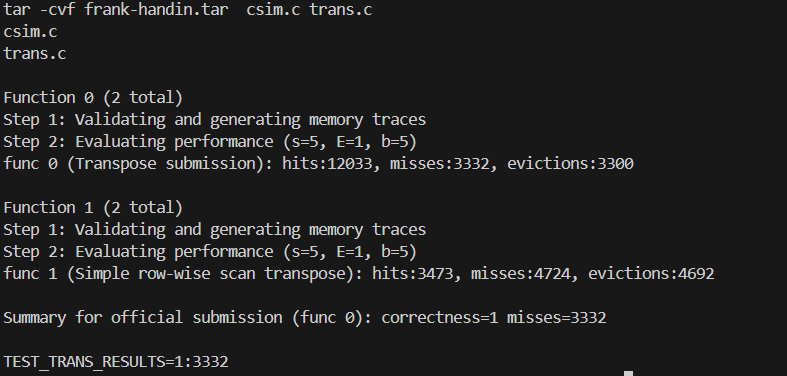
61x67 Matrix Optimization

The matrix dimensions (61 rows, 67 columns) are irregular and not a power of two, making analytical blocking tricky. The cache can still hold 1024 bytes / (67 cols * 4 bytes) ≈ 3.8 full rows of matrix A.

Strategy: Empirical Tuning We can still use blocking, but the optimal block size (size) is found by testing different values to see which minimizes misses under the given constraints (12 variables, no recursion, etc.).

for (int i = 0; i < N; i += size) {
    for (int j = 0; j < M; j += size) {
        // Transpose the `size x size` submatrix, respecting boundaries
        for (int x = i; x < i + size && x < N; ++x) {
            for (int y = j; y < j + size && y < M; ++y) {
                B[y][x] = A[x][y];
            }
        }
    }
}

Final Results and Validation

The implementation for both Part A and Part B was successful, passing all automated tests.