2. 数据结构¶
约 1585 个字 1 张图片 预计阅读时间 8 分钟 共被读过 次
1. Hash Pointers(哈希指针)¶
哈希指针是区块链数据结构中的一个关键概念,它不仅保存了结构体的地址,还保存了该结构体的哈希值。这一特性使得哈希指针能够检测数据是否被篡改。
在区块链中,一个个的区块通过哈希指针连接形成链表结构。其独特之处在于:“block chain is a linked list using hash pointer”(区块链是使用哈希指针的链表),从创世区块(genesis block)开始,一直连接到最新的区块(most recent block)。
好处 - Tamper - Evident Log(防篡改日志)¶
这种基于哈希指针的链表结构形成了一种防篡改日志。因为每个区块的哈希指针不仅指向了前一个区块的地址,还包含前一个区块内容的哈希值。如果对前面任何一个区块的内容进行篡改,该区块的哈希值就会发生变化。由于后续区块的哈希指针依赖于前序区块的哈希值,所以前面区块的任何改动都会导致后面所有区块的哈希指针发生变化,正所谓 “牵一发而动全身”。这样,区块链中的数据一旦被记录,就很难被篡改而不被发现,保证了数据的完整性和可信度。
2. Merkle Tree(默克尔树)¶
默克尔树是一种特殊的二叉树结构,与普通二叉树的区别在于它使用哈希指针代替普通指针。
结构与原理¶
所示,默克尔树的底层节点(data blocks)通常是交易(tx),可以是块头或者块身。其中,块头(block header)包含根哈希值,但不包含交易的具体内容;块身(block body)则包含交易的列表。
好处 - 数据完整性检测¶
默克尔树最大的好处在于,只要知道根哈希(root hash),就能检测出下面任何部分是否发生变化。因为默克尔树的构建方式是将底层节点的哈希值两两组合再进行哈希计算,逐层向上,最终得到根哈希。如果底层任何一个数据块(交易)发生改变,其哈希值就会改变,进而导致上层节点的哈希值也依次改变,最终根哈希值也会不同。所以通过对比当前根哈希值与之前记录的根哈希值,就能判断底层数据是否被篡改。
Merkle Proof(默克尔证明)¶
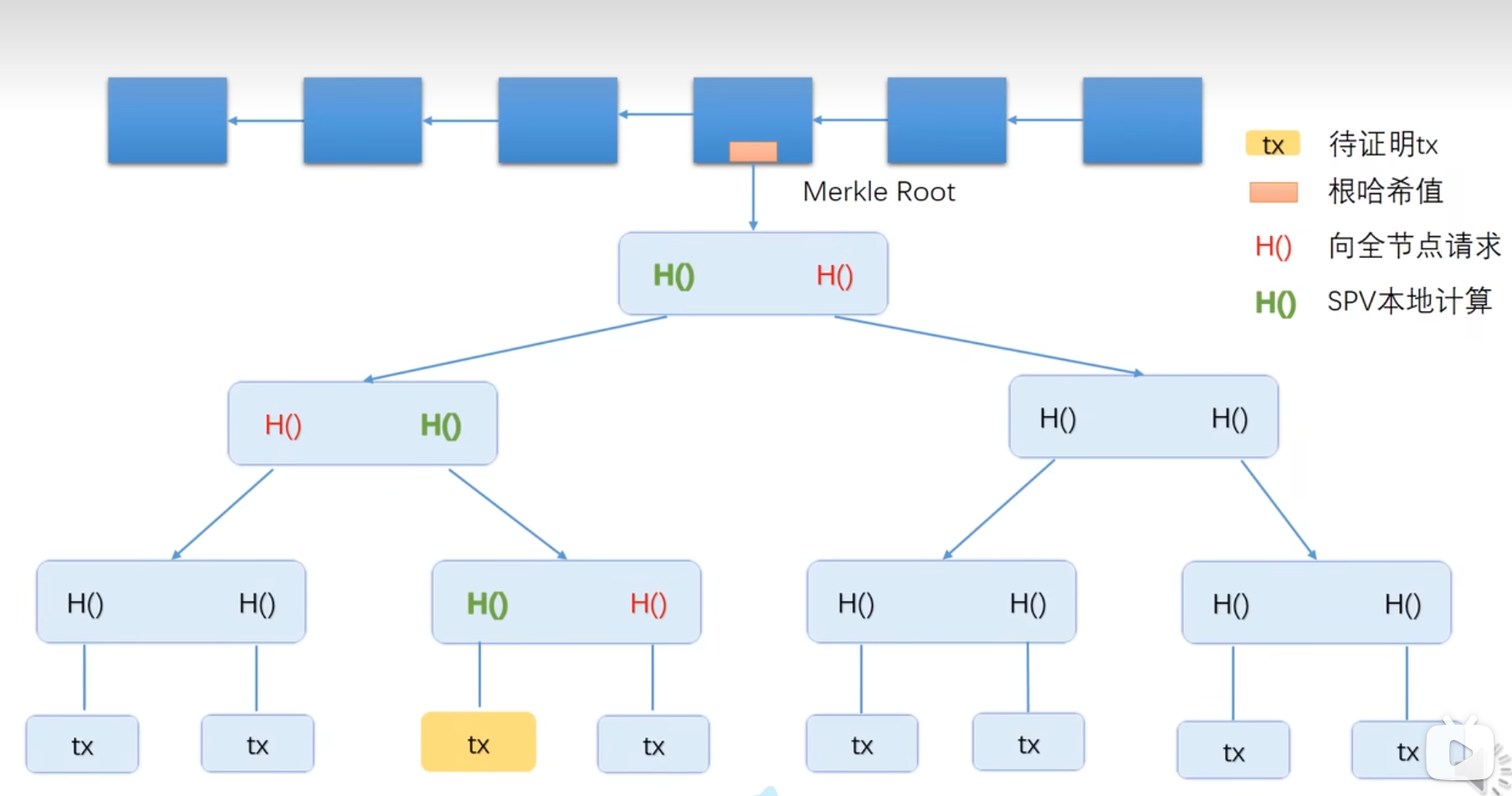
默克尔树提供了默克尔证明机制。在比特币(BTC)中,节点分为两类:全节点和轻节点。全节点保存了完整的区块链数据,包括所有的区块头和区块体;而轻节点只保存一个区块头(block header)。
轻节点相当于手机上的比特币客户端,用户通过轻节点发送交易信息(tx)。由于轻节点没有完整的交易数据,所以它会向全节点请求验证。验证过程中,轻节点通过一层一层的 SPV(Simple Payment Verification,简单支付验证),本地计算部分哈希值,并向全节点请求得到其他哈希值,然后向上一直计算到根哈希,最后将计算得到的根哈希与自己保存的区块头中的根哈希值进行比较,以此判断该交易是否被记录在区块链上。轻节点在验证过程中,只能查询到与该交易相关路径中的哈希值。
安全性分析¶
- 关于篡改证明数据:有人可能会想,能否为了证明自己的交易已记录在区块链上,却又篡改证明过程中需要用到的其他交易,导致证明失败。实际上这种做法是不可行的。因为在默克尔树结构下,若要修改某个节点数据以达到篡改证明的目的,不仅需要修改该节点本身,还需要修改其上层所有依赖该节点哈希值的节点,直至根节点。这意味着几乎要修改整棵树,甚至影响到整条区块链,从算力消耗上来说是不现实的。
- 影响证明正确性的因素:在上述条件下,所提供的默克尔证明中辅助哈希值必然是正确的。因为在正常的区块链网络中,全节点保存的是完整且正确的数据,轻节点从全节点获取的哈希值也是可信的。所以唯一可能影响证明正确性的因素就是验证节点(轻节点)本身,例如其软件实现是否正确、计算过程是否有误等。
成员证明与非成员证明¶
- Proof of Membership(成员证明)/Proof of Inclusion(包含证明):通过默克尔证明可以高效地验证某个交易是否包含在区块链中。由于默克尔树是二叉树结构,从叶子节点到根节点的路径长度为 log (n)(n 为叶子节点的数量),所以验证过程的时间复杂度为 log (n),相对比较高效。
- Proof of Non - Membership(非成员证明):对于证明某个交易不在默克尔树中,传统默克尔树的验证时间复杂度为 n,呈线性关系。但是,如果节点是根据哈希值排好序的(即 sorted merkle tree,排序默克尔树),就可以通过判断某个节点的哈希值在排序中的位置,以及它旁边节点是否相邻,来判断该节点是否在这个树中。不过在比特币的默克尔树中,并不要求节点进行排序。
哈希指针的应用限制¶
哈希指针虽然在区块链数据结构中有诸多优势,但它的应用场景存在一定限制。例如,哈希指针只能用在无环的列表结构中。如果是有环结构,会出现循环依赖的问题,导致哈希值计算无法正常完成,破坏了哈希指针基于数据完整性和顺序性的检测机制。