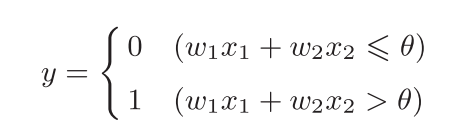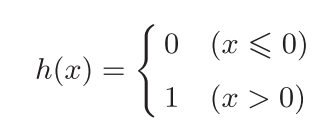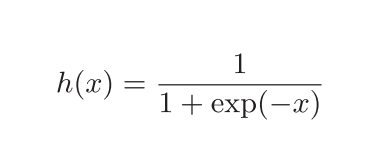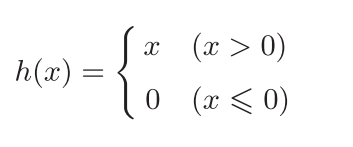深度学习入门:基于python的理论和实现
约 940 个字 38 行代码 20 张图片 预计阅读时间 5 分钟 共被读过 次
1. python入门
1.1 numpy
- numpy是python的一个第三方库,有助于深度学习中数组和矩阵的计算
import numpy as np- 主要的计算方法是对应元素做运算
- 广播:
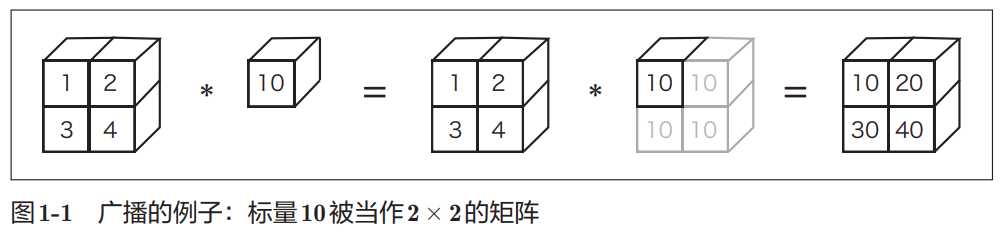
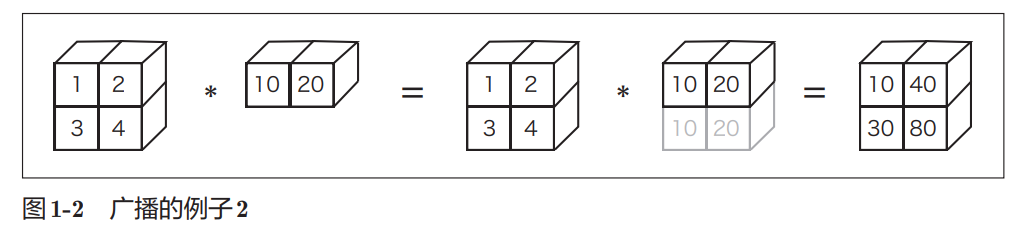
- Python等动态类型语言一般比C和C++等静态类型语言(编译型语言) 运算速度慢。
- 实际上,如果是运算量大的处理对象,用 C/C++写程序更好。为此,当 Python中追求性能时,人们会用 C/C++来实现处理的内容。Python则承担“中间人”的角色,负责调用那些用 C/ C++写的程序。NumPy中,主要的处理也都是通过C或C++实现的。 因此,我们可以在不损失性能的情况下,使用 Python便利的语法。
1.2 Matplotlib
- 用于图形的可视化
- pyplot的功能
Pythonimport numpy as np
import matplotlib.pyplot as plt
x = np.arange(0, 6, 0.01)
y1 = np.sin(x)
y2 = np.cos(x)
# print(x)
# print(y)
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle="--", label="cos")
plt.xlabel("x")
plt.ylabel("y")
plt.title('sin & cos')
plt.legend()
plt.show()
- 运行结果
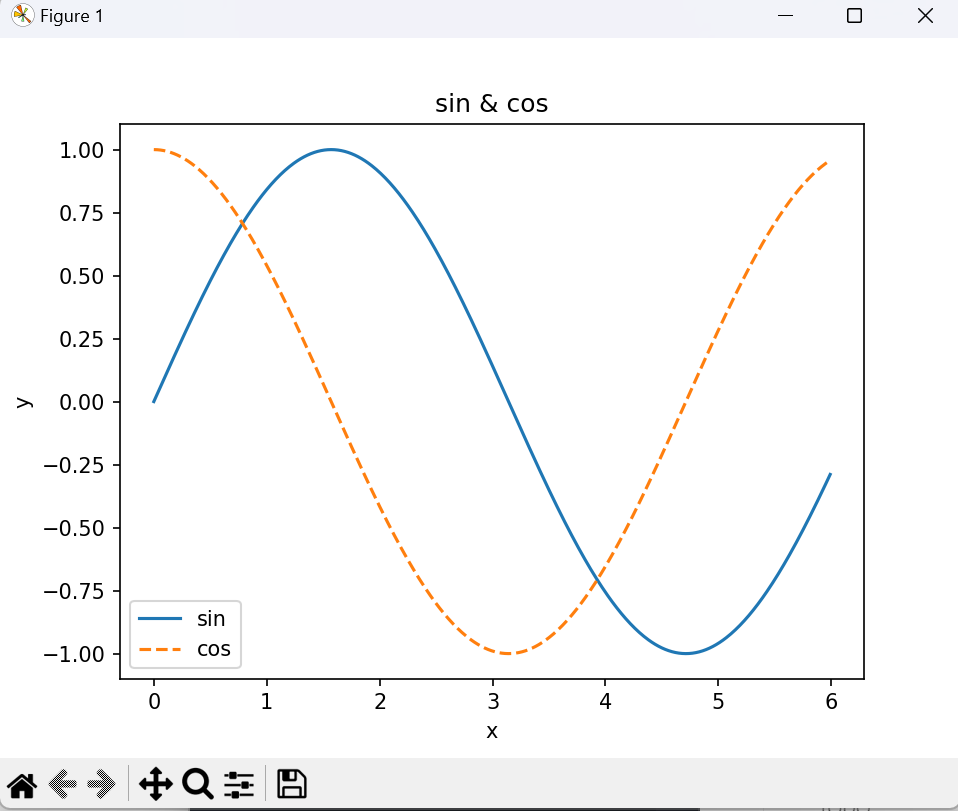
- imshow()函数可以用来读入图像
Pythonimport matplotlib.pyplot as plt
from matplotlib.image import imread
img = imread('lena.png') # 读入图像
plt.imshow(img)
plt.show()
- 运行结果

2. 感知机
2.1 what
-
接受多个信号,输出一个信号
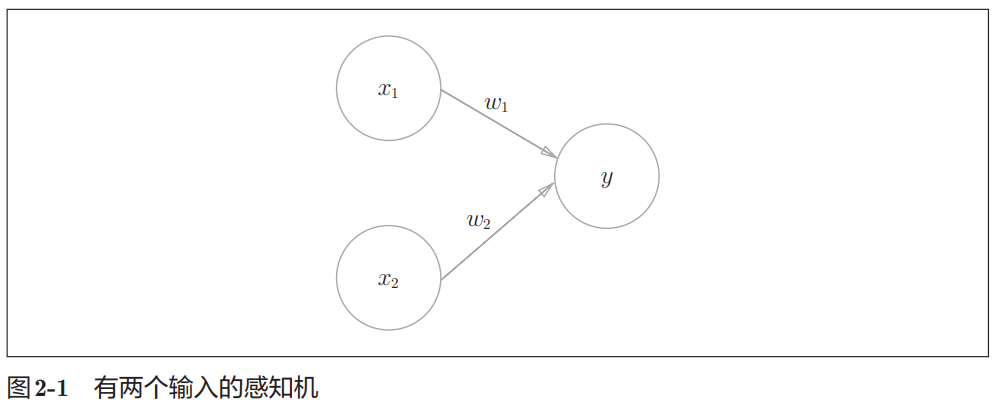
-
有点模拟生物神经元的感觉
- 输入信号乘以对应权重的总和超过阈值的时候 输出1——神经元被激活
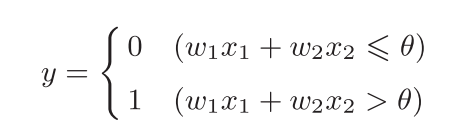
2.2 简单逻辑电路
- 与《code》这本书不同的在于本章以感知机的角度,或者说用python代码的形式去实现逻辑门
- 相同构造的感知机,只需要适当地调整参数的值,就可以在与门、与非门、或门之间转变

2.3 感知机的实现
- 与门
Pythondef AND(x1,x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # w是权重
b = -0.7 # b称为偏置
tmp = np.sum(w * x) + b
return tmp > 0 ? 1 : 0
- 而或门和与非门的实现,仅需改变上面代码中w和b的值即可
2.4 感知机的局限
2.4.1 异或门
- 真值表
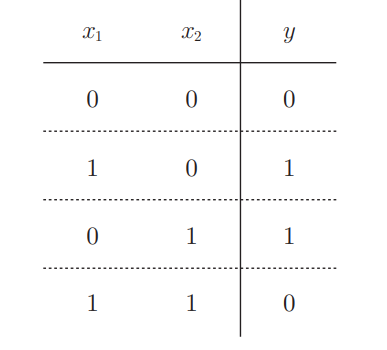
所以我们能找到一组w和b的值,使得简单改变上面代码就能实现异或门吗?- 找不到。为什么找不到呢?通过画图想一下为什么之前3个门是可以的。
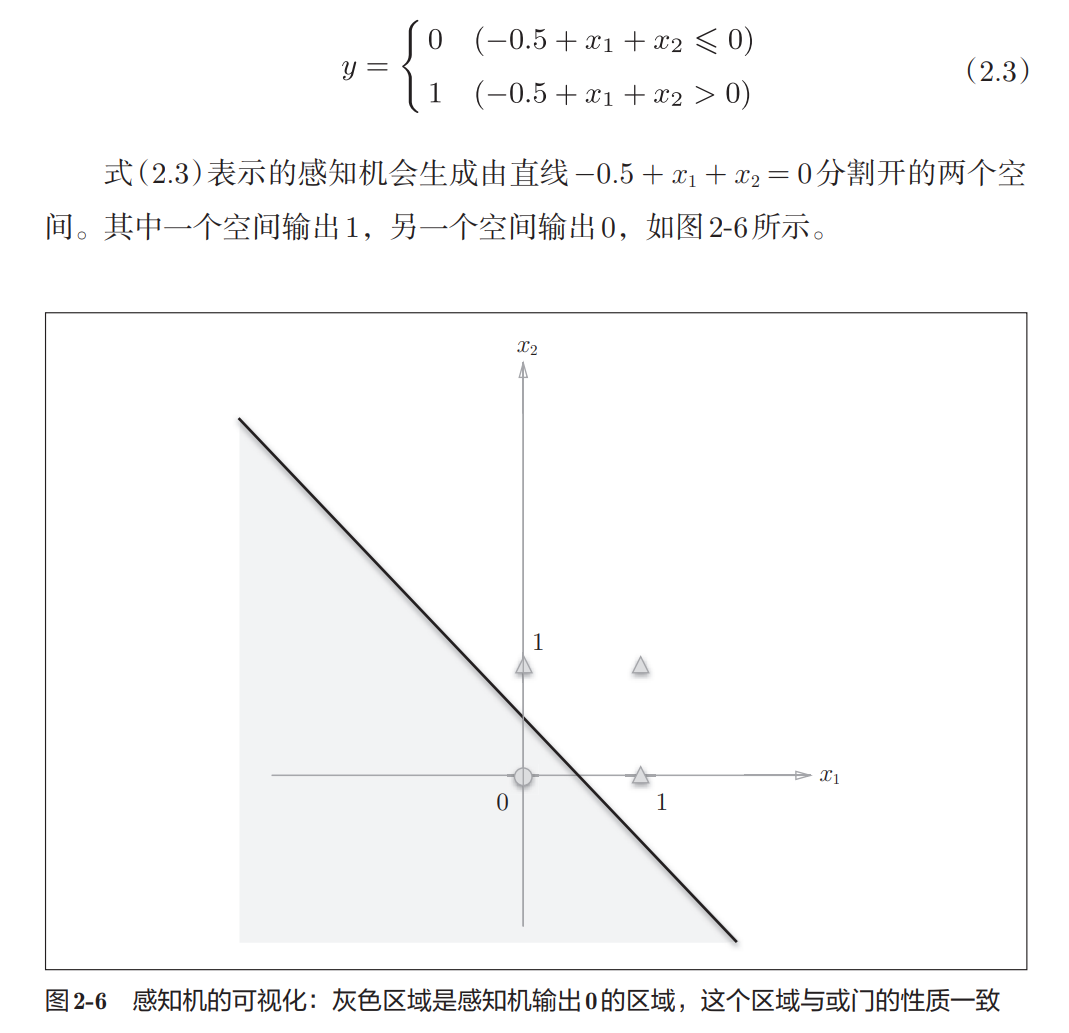
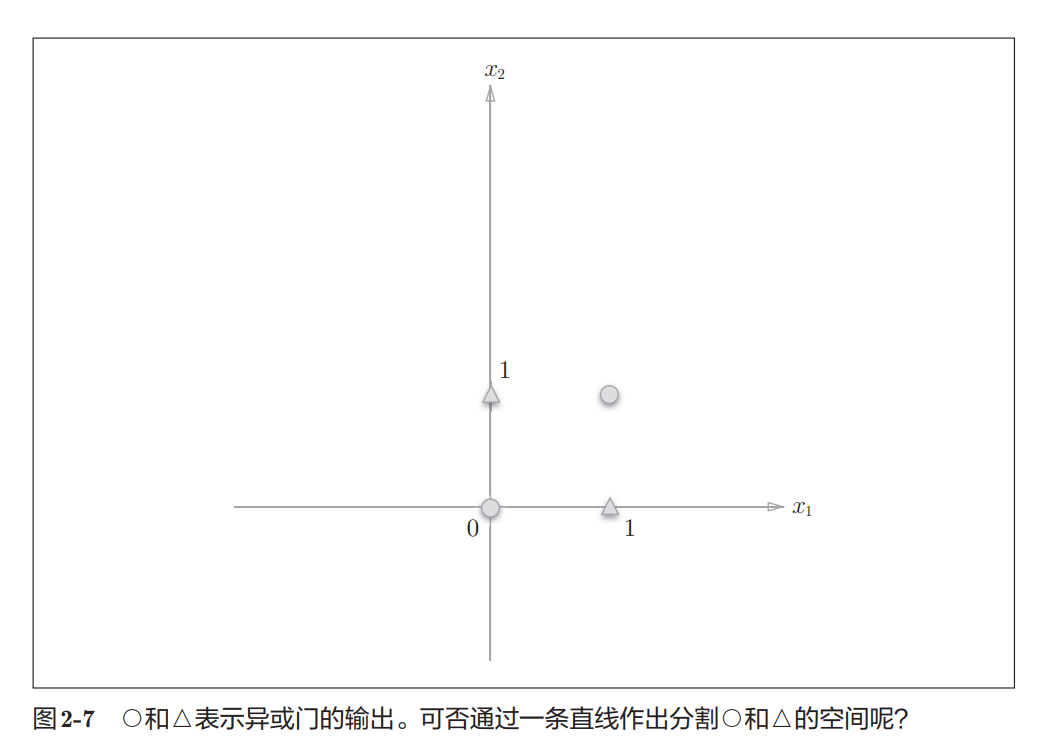
2.4.2 线性和非线性
2.5 多重感知机
2.5.1 已有门电路的组合
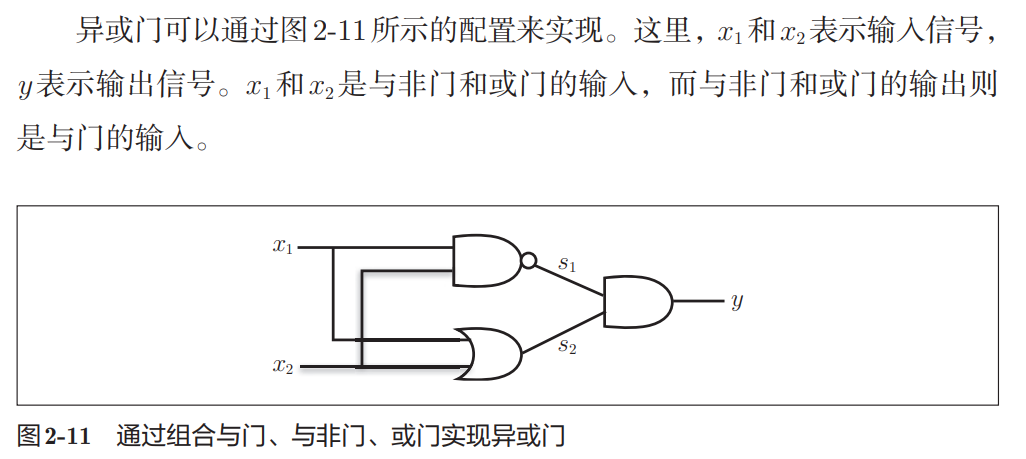
2.5.2 异或门的实现
Pythondef XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
2.6 从与非门到计算机
- 2层感知机(严格地说是激活函数使用了非线性的sigmoid函数的感知机)可以表示任意函数
- 感知机通过叠加层能够进行非线性的表示,理论上还可以表示计算机进行的处理
2.7 小结

3. 神经网络
3.1 从感知机到神经网络
3.1.1 神经网络的例子
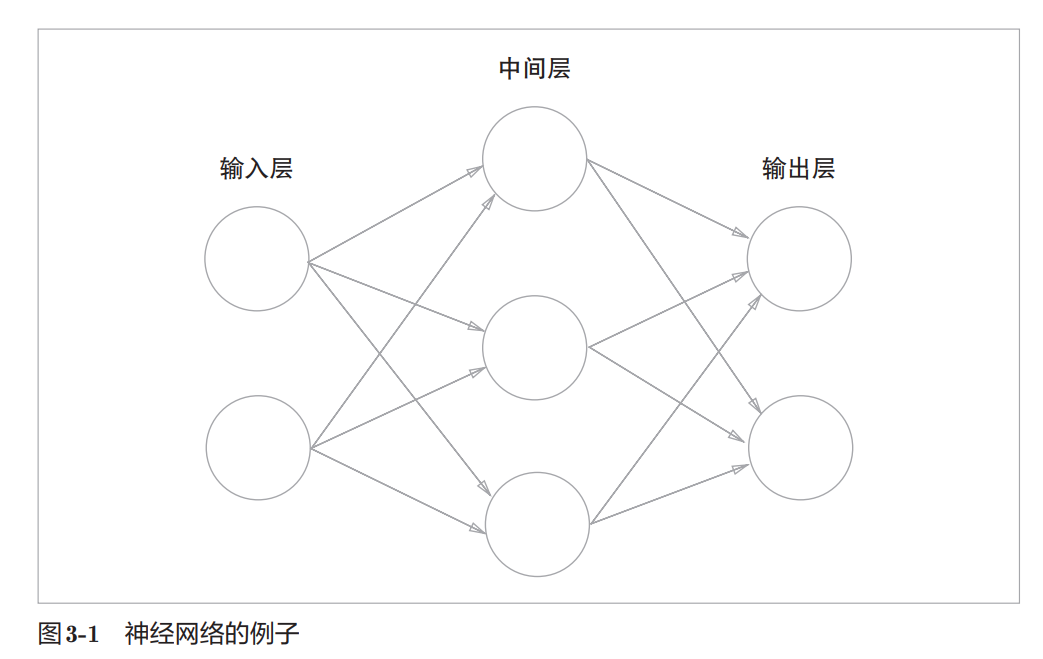
- 神经网络中的信号如何传递呢?
3.1.2 复习感知机
3.1.3 激活函数
- 将输入信号的总和转换为输出信号的函数成为激活函数
- 比如
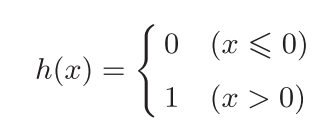
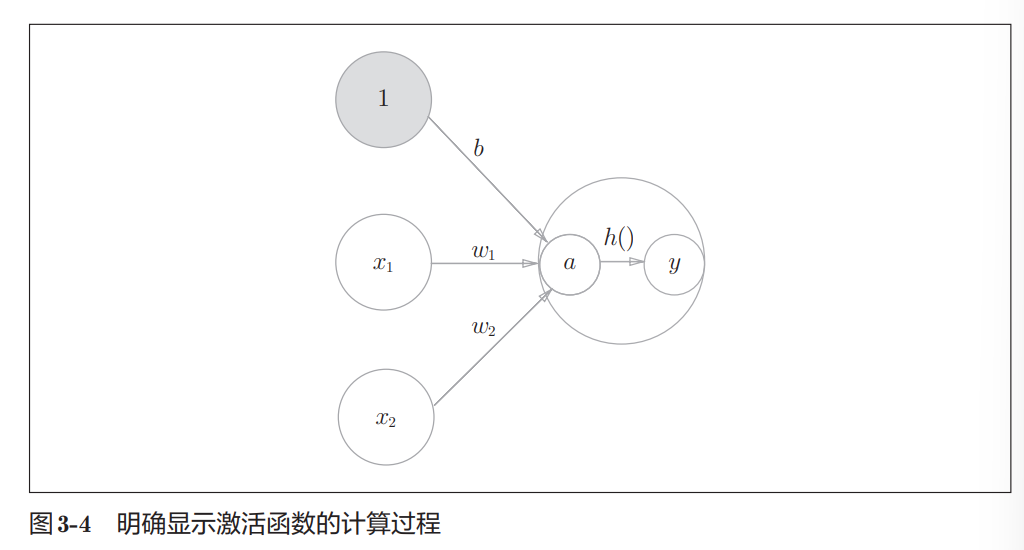
- 激活函数是连接感知机和神经网络的 桥梁。
3.2 激活函数
- 感知机使用阶跃函数作为激活函数,不同于神经网络使用的
3.2.1 sigmoid函数
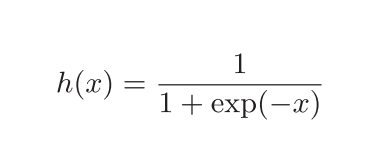
- 特点在于值域在0-1之间,关于(0, 0.5)中心对称
3.2.2 阶跃函数的实现
Pythondef step_function(x):
y = x > 0
return y.astype(np.int)
- 解释:
x > 0 会返回一个布尔类型的Numpy数组,而astype()可以转换Numpy数组的类型为参数指定期望的类型
3.2.3 阶跃函数的图像
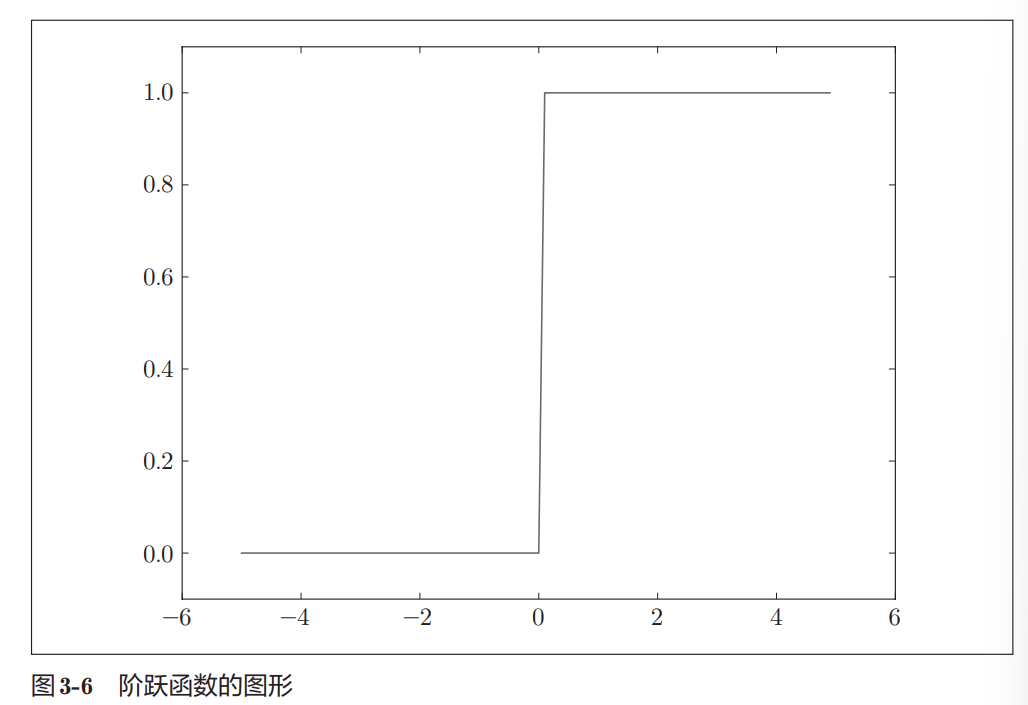
3.2.4 sigmoid函数的实现
Pythondef sigmoid(x):
return 1 / (1 + np.exp(-x))
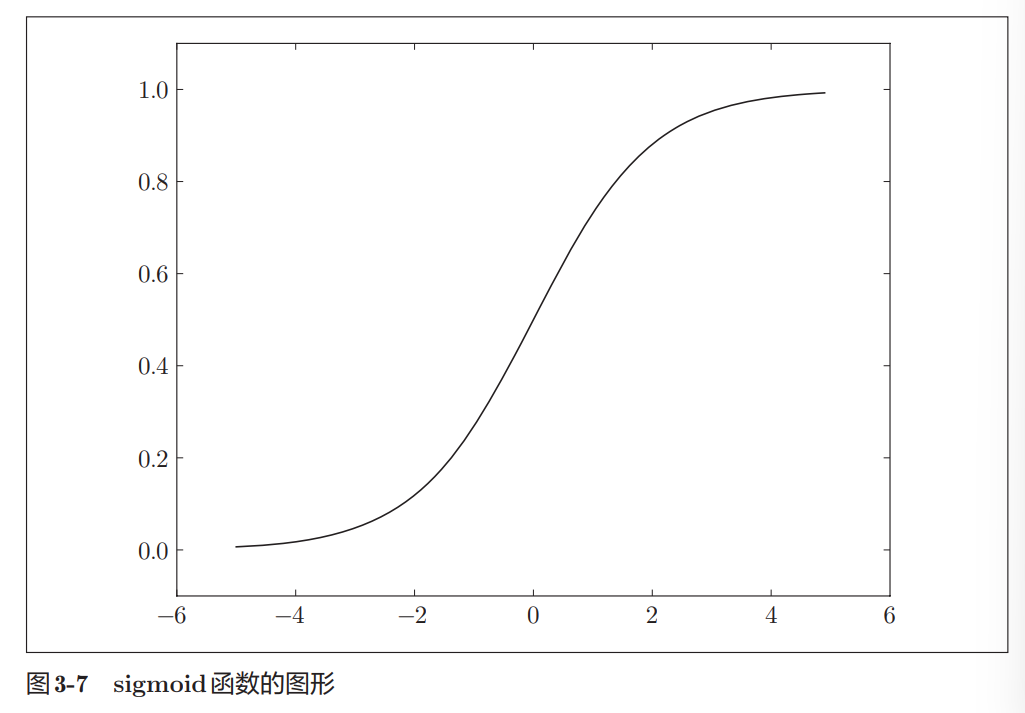
3.2.5 sigmoid函数和阶跃函数的比较
- 连续性和平滑性
- sigmoid会根据输入信号的大小调整输出信号的大小
3.2.6 非线性函数
- 上述二者都是非线性函数
- 线性函数的问题在于,不管如何加深层数,总是存在与之等效的“无 隐藏层的神经网络”。
3.2.7 ReLU函数
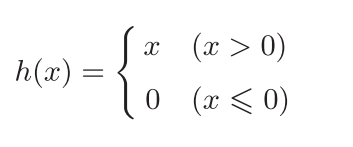
Pythondef relu(x):
return np.maximum(0, x)
3.3 多维数组的运算
3.3.1 多维数组
3.3.2 矩阵乘法
- np.dot(A, B)